Le delta : évaluation des probabilités en fonction du seuil de rentabilité

Comme nous l’avons vu dans un article antérieur, le delta mesure le changement dans le prix de l’option par rapport à un changement dans le prix du titre sous-jacent. Le delta est une variable tirée de la formule d’évaluation des options Black-Scholes qui est aussi utilisée dans l’industrie comme une approximation de la probabilité que l’option soit en jeu à l’échéance*. Ainsi, on dira d’une option fortement en jeu, ayant un delta près de 1, qu’elle a près de 100 % de chance d’être en jeu à l’échéance. Une option fortement hors jeu, ayant un delta près de 0, aura dans ce cas près de 0 % de chance d’être en jeu à l’échéance. Alors qu’une option à parité, ayant un delta près de 0,5, aura à peu près 50 % de chance d’être en jeu à l’échéance.
Prenons l’exemple suivant tiré du calculateur d’options de la Bourse de Montréal.

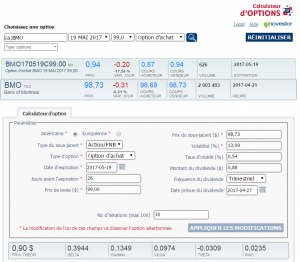
Nous pouvons constater que les options d’achat BMO 170519 C 99.00 ont une valeur théorique de 0,90 $ et un delta de 0,3944. On peut donc dire que cette option d’achat a une probabilité approximative de 39,44 % d’être en jeu à l’échéance, soit de valoir au moins 0,01 $. Or, si j’ai payé 0,90 $ et que l’option n’est en jeu que de 0,01 $ j’encaisserai alors une perte de 0,89 $. Ce que j’aimerais savoir, au moment de l’achat de mon option d’achat, c’est la probabilité que mon option d’achat soit profitable à l’échéance, c’est-à-dire qu’elle soit supérieure à mon seuil d’équilibre de 99,90 $ — prix de levée de 99 $ plus la prime de 0,90 $.
Pour trouver cette probabilité, tout ce qu’on a à faire c’est de trouver le delta d’une option d’achat ayant un prix de levée de 99,90 $. Or, comme ce prix de levée n’est pas disponible dans la liste des prix de levée inscrits à la cote de la Bourse de Montréal, nous allons faire une interpolation à partir du prix de levée le plus près, soit le prix de levée 100 $.

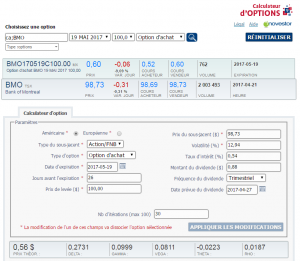
Comme nous pouvons l’observer, l’option d’achat BMO 170519 C 100.00 a un delta de 0,2731, soit une probabilité de 27,31 % d’être en jeu à l’échéance. À partir des données disponibles, nous allons trouver le delta approximatif d’une option d’achat théorique ayant un prix de levée de 99,90 $ — notre seuil d’équilibre — de la manière suivante. À noter que le prix de levée de $99.90 n’existe pas (il n’est pas négociable sur les marchés), l’exercice nous permet uniquement d’estimer les probabilités de succès de notre stratégie.

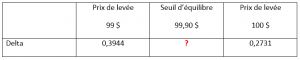
1. Distance entre les prix de levée de référence : 1 $ (100 $ – 99 $)
2. Différence entre les deltas : -0,1213 (0,2731 – 0,3944)
3. Différence entre le seuil d’équilibre et le prix de levée inférieur : 0,90 $ (99,90 $ – 99,00 $
4. Cette différence représente 90 % de la distance entre les prix de levée de référence (0,90 $/1,00 $)
Le delta recherché est obtenu par l’opération suivante :
[(4) 90 % x (2) -0,1213] + [delta du prix de levée inférieur] 0,3944 = -0,10917 + 0,3944 = 0,2852

Par conséquent, on peut dire qu’en achetant les options d’achat BMO 170519 C 99.00 à 0,90 $ on a approximativement 28,52 % de chance de réaliser un profit. Nous savons que les probabilités que le prix de BMO soit supérieur à 99 $ sont de 39,44 %. Par conséquent, nous pouvons donc dire que les probabilités que le prix soit inférieur à 99 $ sont de 60,56 % [1 – 0,3944]. Or, cela veut dire qu’on a 60,56 % de chance de subir une perte totale. Ainsi, nous avons maintenant plusieurs informations importantes nous permettant de déterminer si nos chances de réussite sont satisfaisantes et si nos objectifs sur le titre sous-jacent sont réalistes à long terme. Cette procédure peut être utilisée pour approximer les probabilités d’être profitable pour toutes les stratégies que nous mettons en place, des écarts simples aux plus complexes.

Bonnes transactions et bonne semaine !

* Bien que le delta soit utilisé comme une bonne approximation de la probabilité que l’option soit en jeu à l’échéance, en réalité il existe une autre variable qui nous donne de manière plus précise cette probabilité. On utilise le delta, car il est facilement accessible dans les logiciels d’options fréquemment utilisés.
Formule Black-Scholes pour une option d’achat1 c = S0 * N(d1) – VA(K) * N(d2)
1 Option d’achat de style américain ou européen sur des actions qui ne versent pas de dividendes d’ici l’échéance.
Où : c = option d’achat
S0 = prix actuel du titre sous-jacent
VA(K) = valeur actuelle du prix de levée
N(d1) et N(d2) sont des fonctions de répartition d’une loi normale centrée-réduite exprimant la probabilité qu’une variable suivant une loi normale soit inférieure à d1 et d2
C’est N(d1) qui représente le delta alors que N(d2) représente actuellement la probabilité que l’option soit en jeu à l’échéance. De manière générale, le delta d’une option sera plus élevé que la probabilité d’être en jeu, et cette différence devient de plus en plus importante, plus l’échéance des options est longue et que la volatilité sur le titre sous-jacent est élevée.

Les stratégies présentées dans le cadre de cette chronique ne le sont qu’à titre d’information et de formation et ne doivent pas être interprétées comme étant des recommandations pour acheter ou vendre toutes valeurs mobilières. Comme toujours, avant de mettre en place des stratégies d’options assurez-vous d’être à l’aise avec les scénarios proposés et d’être prêts à en assumer tous les risques.